张量结构与所有权
在 Rust 中,所有权和生命周期 (与视窗的概念相关) 有严格的规则。了解数据 (譬如大量浮点数的内存) 是如何存储和处理的,以及一个变量是拥有还是引用这些数据,是非常重要的。
作为一个张量库,我们也希望有一些统一的 API 函数或操作,能够同时处理拥有数据本体、和引用数据的张量的计算。通俗地说,NumPy 非常方便,我们可能希望在 Rust 中以类似 Python 的方式编写代码。
在本节中,我们将尝试展示 RSTSR 如何构建张量结构,以及不同所有权的张量是如何工作的。
1. 张量结构
RSTSR 张量从 Rust 库 ndarray 中学到了很多。RSTSR 的 TensorBase 的结构和使用方式与 ndarray 的 ArrayBase 类似;然而,它们在许多关键点上有所不同。
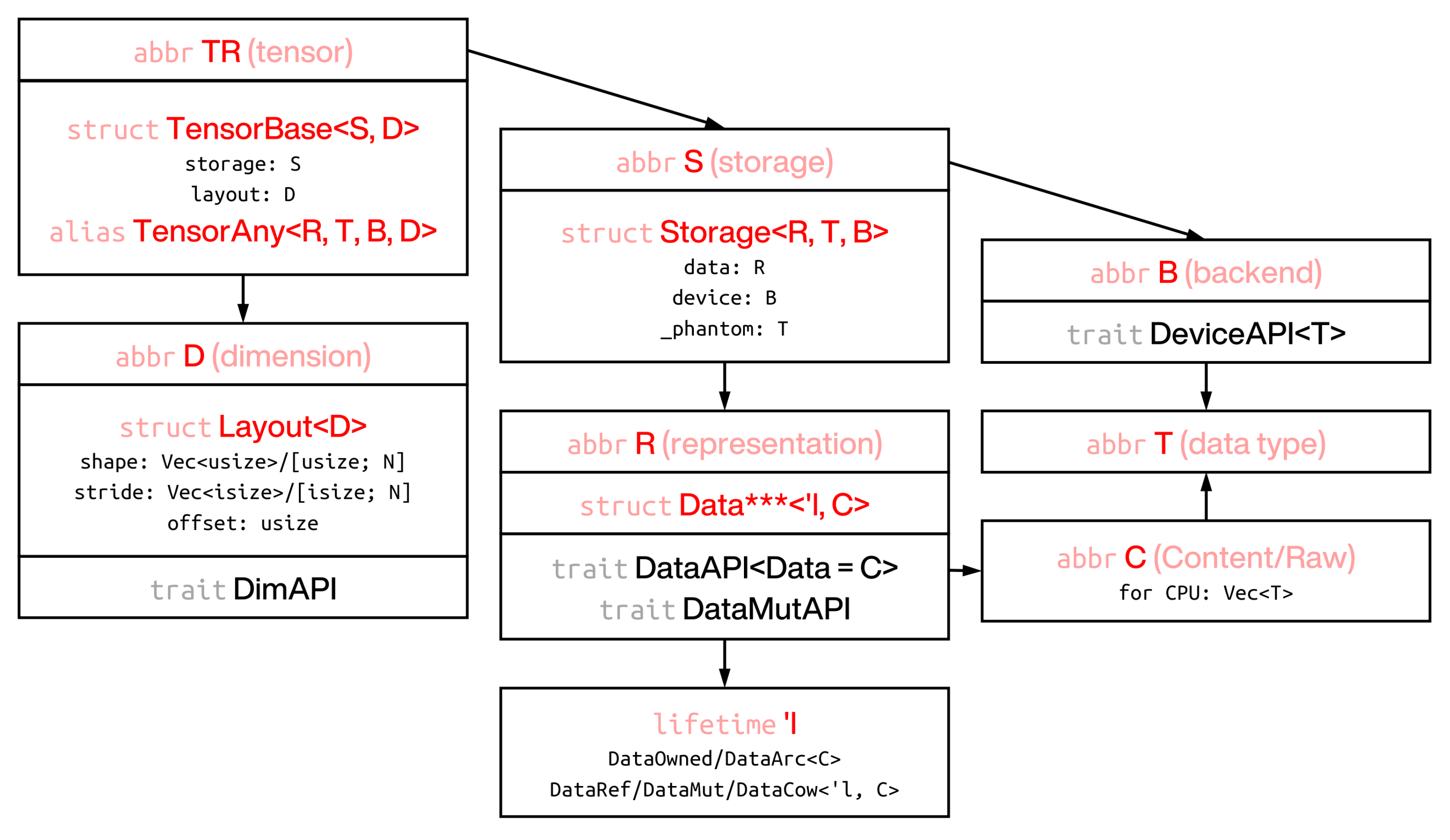
- 张量由
storage(数据在内存块中的存储方式) 和layout(张量的表示方式) 组成。 - Layout 由
shape(张量的形状) 、stride(如何从内存块中访问每个值) 和offset(张量的起始位置) 组成1。 - Storage 由
data(带有生命周期的数据) 和device(计算和存储后端) 组成2。 - Data 是实际内存存储与生命周期注解的组合。目前支持 5 种所有权类型。前两种 (拥有和引用) 是最重要的3。
- 拥有 (
Tensor<T, B, D>) - 引用 (
TensorView<'l, T, B, D>或TensorRef<'l, T, B, D>) - 可变引用 (
TensorViewMut<'l, T, B, D>或TensorMut<'l, T, B, D>) - 写时克隆 (不可变枚举,表示拥有或引用的状态,
TensorCow<'l, T, B, D>) - 原子引用计数 (线程安全,
TensorArc<T, B, D>)
- 拥有 (
- 如果后端是 CPU 设备,那么实际的内存块将作为
Vec<T>;对于其他后端设备,这可以通过 trait 类型DeviceRawAPI<T>::Raw进行配置4。
默认的泛型类型应用于某些结构体或别名。例如,如果 DeviceFaer 是默认设备 (通过 crate 特性 faer_as_default 启用),那么:
let a: Tensor<f64> = rt::zeros([3, 4]);
// 这指的是 Tensor<f64, DeviceFaer, IxD>
// 默认设备:DeviceFaer (使用 Faer 矩阵乘法的 rayon 并行,需要 feature `faer_as_default`)
// 默认维度:IxD (动态维度)
2. 所有权转换
2.1 张量所有权之间的转换
不同的所有权可以相互转换。然而,某些转换函数可能会有一些成本 (显式的内存复制) 。
view生成TensorView<'l, T, B, D>。- 此函数在任何情况下都不会执行张量数据的内存复制。在这方面,它几乎是零成本的。
- 它仍然会执行张量 layout 的克隆,因此仍有一些开销。对于大型张量来说,这是廉价的。
view_mut生成TensorMut<'l, T, B, D>。- 在 Rust 中,要么允许多个不可变引用,要么只允许一个可变引用。对于
TensorView作为不可变引用和TensorMut作为可变引用也是如此。
- 在 Rust 中,要么允许多个不可变引用,要么只允许一个可变引用。对于
into_owned_keep_layout生成Tensor<T, B, D>。- 对于
Tensor,这不会进行内存复制; - 对于
TensorView和TensorMut,这需要显式的内存复制。请注意,在这种情况下通常更适合使用into_owned。 - 对于
TensorArc,这不会进行内存复制,但请注意,当强引用计数不恰好为 1 时,它可能会 panic。您可以使用tensor.data().strong_count()来检查强引用计数。 - 对于
TensorCow,如果它是拥有的 (DataCow::Owned),则不会进行内存复制;如果它是引用的 (DataCow::Ref),则需要显式的内存复制。
- 对于
into_owned也生成Tensor<T, B, D>。- 此函数与
into_owned_keep_layout不同,因为into_owned仅在张量的 layout 覆盖所有内存 (内存块的大小与张量 layout 的大小相同) 时不会复制内存。对任何非平凡的张量切片调用into_owned都会导致内存复制。 - 还要注意,如果您只想将内存缩小到张量的一个切片,使用
into_owned更合适。 - 对于
TensorView和TensorMut,使用into_owned会比into_owned_keep_layout复制更少的内存。因此,对于张量视窗,更建议使用into_owned。
- 此函数与
into_cow生成TensorCow<'l, T, B, D>。- 此函数没有任何成本。
into_shared_keep_layout和into_shared生成TensorArc<'l, T, B, D>。这与into_owned_keep_layout和into_owned类似。
以下是一个张量所有权转换的示例:
// generate 1-D owned tensor
let tensor = rt::arange(12);
let ptr_1 = tensor.as_ptr();
// this will give owned tensor with 2-D shape
// since previous tensor is contiguous, this will not copy memory
let mut tensor = tensor.into_shape([3, 4]);
tensor += 1; // inplace operation
let ptr_2 = tensor.as_ptr();
// until now, memory has not been copied
assert_eq!(ptr_1, ptr_2);
// convert to view
let tensor_view = tensor.view();
// from view to owned tensor
let tensor = tensor_view.into_owned();
let ptr_3 = tensor.as_ptr();
// now memory has been copied
assert_ne!(ptr_2, ptr_3);
2.2 张量与 Vec<T> 的转换
我们已经在 上一节 中介绍了一些通过数组创建函数的方法。这里我们将进一步讨论这个话题。
在以下情况下,张量与 Vec<T> 或 &[T] 之间的转换可能很有用:
- 将数据传输到其他对象 (如 candle、ndarray、nalgebra);
- 需要指针来执行 FFI 操作 (如 BLAS、Lapack);
- 导出数据以进行进一步的序列化。
有一些有用的函数可以执行张量到 Vec<T> 的转换:
to_vec():将 1-D 张量复制到向量,需要内存复制;into_vec():如果张量在内存上是连续的,则将 1-D 张量移动到向量;否则将 1-D 张量复制到向量。
我们不提供直接返回 &[T] 或 &mut [T] 的函数。然而,我们提供了 as_ptr() 和 as_mut_ptr() 函数,返回内部内存中的第一个元素的指针。
请注意,上述提到的实用程序仅在 CPU 上有效。对于其他设备 (将在未来实现),您可能希望首先将张量转换为 CPU,然后执行张量到 Vec<T> 的转换。
作为一个示例,我们计算矩阵-向量乘法并返回 Vec<f64>:
// generate *dynamic* 2-D tensor (vec![3, 4] is dynamic)
let a = rt::arange(12.0).into_shape(vec![3, 4]);
let b = rt::arange(4.0);
// matrix multiplication (gemv 2-D x 1-D case)
let c = a % b;
println!("{:?}", c);
let ptr_1 = c.as_ptr();
// convert to Vec<f64>
let c = c.into_vec();
let ptr_2 = c.as_ptr();
println!("{:?}", c);
println!("{:?}", core::any::type_name_of_val(&c));
assert_eq!(c, vec![14.0, 38.0, 62.0]);
// memory has been moved and no copy occurs if using `into_vec` instead of `to_vec`
assert_eq!(ptr_1, ptr_2);
函数 as_ptr() 与 as_mut_ptr() 会返回张量的内存的第一个元素的指针;但需要注意到,该指针指向的张量未必是连续的。RSTSR 在给出指针时,不会检查张量是否连续。
let a = rt::arange(12.0).into_shape([3, 4]);
let a_ptr = a.as_ptr();
println!("{:}", a);
// output: [[ 0 1 2 3]
// [ 4 5 6 7]
// [ 8 9 10 11]]
// please note that b is not contiguous
// be careful if you want to use `as_ptr` on non-contiguous tensor
let b = a.i(slice!(1, None, -1));
let b_ptr = b.as_ptr();
println!("{:}", b);
// output: [[ 4 5 6 7]
// [ 0 1 2 3]]
println!("{:}", unsafe { a_ptr.offset_from(b_ptr) });
// output: -4
2.3 张量与标量的转换
RSTSR 不提供直接将 T 转换为 0-D 张量 Tensor<T, Ix0, B> 的方法。对于将 0-D 张量 Tensor<T, Ix0, B> 转换为 T,我们提供了 to_scalar 函数。
作为一个示例,我们计算内积并返回浮点数结果:
// a: [0, 1, 2, 3, 4]
let a = rt::arange(5.0);
// b: [4, 3, 2, 1, 0]
let b = rt::arange(5.0);
let b = b.slice(slice!(None, None, -1)); // or b.flip(0)
// matrix multiplication (dot product for 1-D case)
let c = a % b;
// to now, it is still 0-D tensor
println!("{:?}", c);
// convert to scalar
let c = c.to_scalar();
println!("{:?}", c);
assert_eq!(c, 10.0);
3. 维度转换
RSTSR 提供了固定维度和动态维度的张量。维度可以通过 into_dim::<D>() 或 into_dyn 进行转换。
// fixed dimension
let a = rt::arange(12).into_shape([3, 4]);
println!("{:?}", a);
// output: 2-Dim (dyn), contiguous: Cc
// convert to dynamic dimension
let a = a.into_dim::<IxD>(); // or a.into_dyn();
println!("{:?}", a);
// output: 2-Dim (dyn), contiguous: Cc
// convert to fixed dimension again
let a = a.into_dim::<Ix2>();
println!("{:?}", a);
// output: 2-Dim, contiguous: Cc
我们只讨论了固定维度的数组创建。要创建动态维度的数组,请使用 Vec<T> 而不是 [T; N]:
let a = rt::arange(12).into_shape(vec![3, 4]);
println!("{:?}", a);
// output: 2-Dim (dyn), contiguous: Cc
固定维度比动态维度更高效。然而,在许多算术计算中,取决于张量的连续性,效率差异不会非常显著。同时,rstsr 提供了 dispatch_dim_layout_iter cargo 选项;这使得在较大张量的计算中,动态维度的计算效率与固定维度相当。
考虑到动态维度的计算效率一般并不显著低于固定维度,我们推荐 RSTSR 用户积极使用动态维度。
对于维度,RSTSR 使用了与 Rust 库 ndarray 类似的解决方案,即提供固定维度与动态维度两种选择。固定维度意味着 -D 张量的 在编译时是固定的。这与 numpy 不同,后者的维度始终是动态的。
RSTSR 与 Rust 库 nalgebra 和 dfdx 非常不同;这些 Rust 库支持固定的 shape 和 strides。也就是说,不仅维度 是固定的,而且 shape 和 strides 在编译时也是已知的。对于小向量或矩阵,固定 shape 和 strides 通常可以编译为更高效的汇编代码。对于大向量或矩阵,这将取决于算术计算的类型;带有 -O3 的编译器并不是全知全能的,在大多数情况下,固定 shape 和 strides 不会比动态维度下利用多级缓存、流水线和多线程优化带来更多的好处。编写一个更高效的函数比告诉编译器张量的维度更可取。
RSTSR 的设计和动机是用于中等或大型张量的科学计算。考虑到好处和困难,我们选择不引入固定的 shape 和 strides。这使得 RSTSR 不适合处理小矩阵的任务 (如游戏和着色)。对于某些对特定任务 (如深度学习中 CNN 涉及滤波器的计算),RSTSR 适合用于张量存储,用户可能希望使用自定义的计算函数而不是 RSTSR 的函数来执行计算密集型部分。
Footnotes
-
RSTSR 在结构构造上与 ndarray 不同。虽然 ndarray 直接在
ArrayBase中存储 shape 和 stride,但在 RSTSR 中,shape、stride 和 offset 存储在Layout<D>中。张量的 layout 是张量的元数据,它可以与张量的数据分离。 ↩ -
这是 RSTSR 与 ndarray 的区别之一。我们希望 RSTSR 在未来成为一个多后端的框架。目前,我们已经实现了串行 CPU 设备 (
DeviceCpuSerial) 和带有 Faer 矩阵乘法的并行 CPU 设备 (DeviceFaer),展示了在 RSTSR 框架内进行更复杂的异构编程的可能性。 ↩ -
在 RSTSR 中,数据以变量或其引用的形式存储,符合 Rust 的安全规则。这与 ndarray 不同,后者存储指针 (带有 offset) 和内存数据 (如果拥有) 或虚拟生命周期注解 (如果引用) 。 ↩
-
这是 RSTSR 与 candle 的区别之一。RSTSR 允许外部实现后端,希望可以轻松扩展到其他类型的设备,类似于 burn。RSTSR 还允许几乎所有类型的元素类型 (您可以将
rug甚至Vec<T>作为张量元素,只要它们实现了Clone),类似于 ndarray。然而,RSTSR 可能不会在未来实现自动微分,这是与 candle 和 burn 相比的缺点。 ↩